Persamaan Garis Singgung Lingkaran

Melalui Titik	Persamaan Lingkaran	Titik Pusat Lingkaran	Persamaan Garis Singgungnya
Titik P (x1,y1)	x2+y2=r2	(0,0)	x1x+y1y= r2
Titik P (x1,y1)	(x-a)2+(y-b)2=r2	(a,b)	(x1-a) (x-a)+(y1-b) (y-b)= r2
Titik P (x1,y1)	x2+y2+2Ax+2By+C= 0	(-A,-B)	x1x+y1y+A(x1x)+b(y1y)+C =0

Contoh Soal 1

Jika sebuah garis menyinggung lingkaran di titik (-8,6) dan lingkaran tersebut mempunyai persamaan x²+y²=100. Tentukan persamaan dari garis tersebut?

Jawab : caranya cukup mudah tinggal masukkan ke rumus persamaan garis singgung lingkaran yang pertama
x₁x+y₁y= r²
-8x+6y = 100
-4x+3y = 50

Contoh Soal 2
tentukan persamaan garis singgung lingkaran (x-4)² + (y-3)² = 36 di titik (-2,1)

Jawab
(x₁-a) (x-a)+(y₁-b) (y-b)= r²(-2-4) (x-4) + (1-3) (y-3)  = r²
-6 (x-4) + -2(y-3) = 36
-6x+24 -2y+6 = 36
-6x -2y +30 = 36
-6x – 2y = 6
-3x -y – 3=0

Contoh Soal 3

Coba sobat hitung tentukan persamaan gari singgung lingkaran x²+y²+8x-6y+9 = 0 pada titik (-2,5)
Jawab, sama seperti soal-soal sebelumnya sobat tinggal memasukkan ke rumus
dar soal di atas dapat diketahui (-2,5) maka x₁ = -2 dan y₁ = 5
dari x²+y²+8x-6y+9 = 0 dapat diketahui A = 4, B = -3, dan C =9

x₁x+y₁y+A(x₁x)+b(y₁y)+C =0
-2x+5y+4(-2x)-3(5y)+9 = 0
-2x+5y-8x-15y+9 = 0
-10x-10y+9 =0
Sekarang ada pertanyaan, bagaimana cara menentukan persamaan suatu garis singgung lingkaran jika yang diketahui adalah grdiennya bukan titik singgungnya? untuk bisa menjawab pertanyaan tersebut berikut penjelasannya.

Persamaan Garis Singgung Lingkaran Jika Gradiennya Diketahui

Gradien	Persamaan Lingkaran	Titik Pusat Lingkaran	Persamaan Garis Singgungnya
m	x2+y2=r2	(0,0)
m	(x-a)2+(y-b)2=r2	(a,b)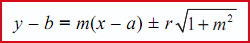
m	x2+y2+2Ax+2By+C= 0	(-A,-B)

Contoh Soal
Tentukan persamaan garis singgung lingkaran x²+y²+4x-2y+1=0 yang tegak lurus dengan garis z -3x+4y-1=0

Jawaban :

Langkah Pertama : Tentukan gradien garis singgung lingkaran

“tegak lurus dengan garis -3x+4y-1=0″ maka berlaku
m1 x m2 = -1
-3x+4y-1=0 ⇔4y = 3x + 1 ⇔ m = 3/4
m1 x 3/4 = -1
m1 = -4/3 (gradien garis singgung lingkaran)

Langkah Kedua : tentukan nilai r

dari persamaan x²+y²+4x-2y+1=0 di dapat titik pusa (a,b) yaitu (-2,1), a =-2, b =1, c =1

r² = a²+b²-c
r² = (-2)²+1²-1
r² = 4
r = 2 (-2 tidak masuk karena jari-jari tidak bisa bernilai negatif)

Langkah Ketiga : masukkan ke dalam rumus

Buat sobat hitung, saya sarankan jangan berusaha menghafal rumus persamaan garis singgung lingkaran yang cukup banyak. Coba coba saja dipahami dan cara paling cepat memahami adalah mencoba latihan soal matematika tentang materi ini. Selamat Belajar, semoga bermanfaat.

sumber =http://rumushitung.com/2013/07/20/persamaan-garis-singgung-lingkaran/